第一次找到和我要做的课题那么接近的教程，人工翻译一遍不过分吧！😎
本文对应的代码在这里！😽[Open in colab]😽

任务优化的循环神经网络建模

引言

这里，我们基于人工神经网络的方法构建循环神经网络。学习人工神经网络或深度学习，不仅是当今机器学习的主导框架，对计算神经科学而言也是一个有用的工具。

深度学习本身可能并不符合生物现实。然而，深度学习最终的结果可能是有用的大脑模型（不保证，但是可能）。由于人工神经网络的复杂性，它们可以模拟复杂的行为和神经活动。

从优化的角度来说，人工神经网络建模可以提供规范性解释，即为什么一个网络可以以某种方式完成某个任务，因为我们可以设计目标函数，类似于生物进化的视角。

任务介绍

2AFC

双向强迫选择任务PerceptualDecisionMaking，被试需要整合两个刺激来决定哪一个刺激的平均水平更高。
在刺激阶段会呈现一个有噪声的刺激。刺激的强度（coherence）在每个试次中是随机抽样的。因为刺激中存在噪声，智能体需要随时间整合刺激信息。
参数介绍：
dt：Timestep duration. (def: 100 (ms) int)
rewards：

  • R_ABORTED: given when breaking fixation. (def: -0.1 float)
  • R_CORRECT：given when correct. (def: +1. float)
  • R_FAIL：given when incorrect. (def: 0. float)

timing：Description and duration of periods forming a trial.
stim_scale：Controls the difficulty of the experiment. (def: 1., float)
cohs：list of float, coherence levels controlling the difficulty of the task
sigma：float, input noise level
dim_ring：int, dimension of ring input and output

环境配置

  • NeuroGym是一个精选的神经科学任务集合，具有统一的接口。其目标是促进关于神经科学任务的神经网络模型的训练。
    NeuroGym
  • Google Colab是一个基于云端的免费Jupyter笔记本环境，为用户提供了方便、免费的编码环境，并具备强大的计算资源和协作功能，适用于数据科学家、研究人员和机器学习工程师等进行代码开发、实验和协作。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    # install neurogym (for training environments)
    ! git clone https://github.com/gyyang/neurogym.git
    %cd neurogym
    ! pip install -e .

    # import packages
    import time # for measuring time
    import numpy as np # for numerical computation
    from matplotlib import cm # for plotting figures
    import matplotlib as mpl
    import matplotlib.pyplot as plt
    from matplotlib.colors import ListedColormap, LinearSegmentedColormap
    from matplotlib.lines import Line2D
    from IPython import display # for controlling colab

    import gym # for neurogym
    import neurogym as ngym # for training environments
    import torch # for training neural nets
    import torch.nn.functional as F

    from sklearn.decomposition import PCA # for principal component analysis
    from scipy.special import softmax
    mpl.rcParams.update(mpl.rcParamsDefault)

模型概览

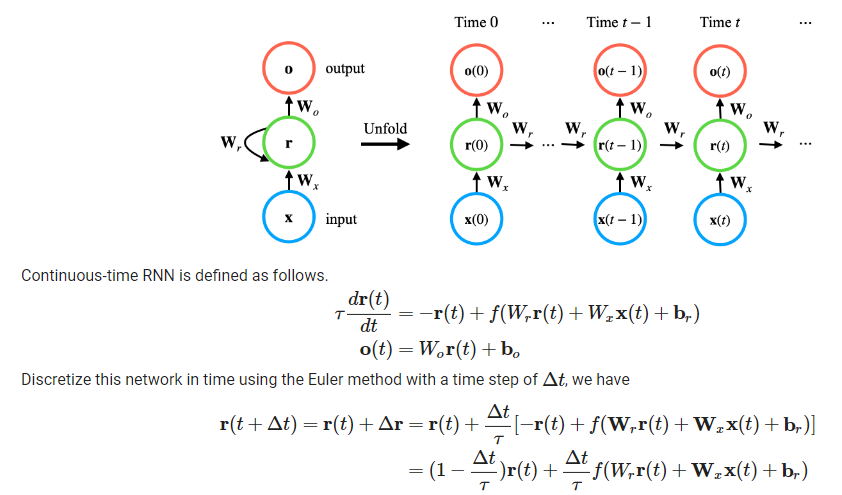
RNN模型概览

$x(t)$：输入变量

$r(t)$：循环变量

$o(t)$：输出

$W_x$：输入权重【可训练】

$W_r, b_r$：循环权重 & 偏置

$W_o, b_o$：输出权重 & 偏置

$\alpha=\frac{\bigtriangleup t}{\tau }$

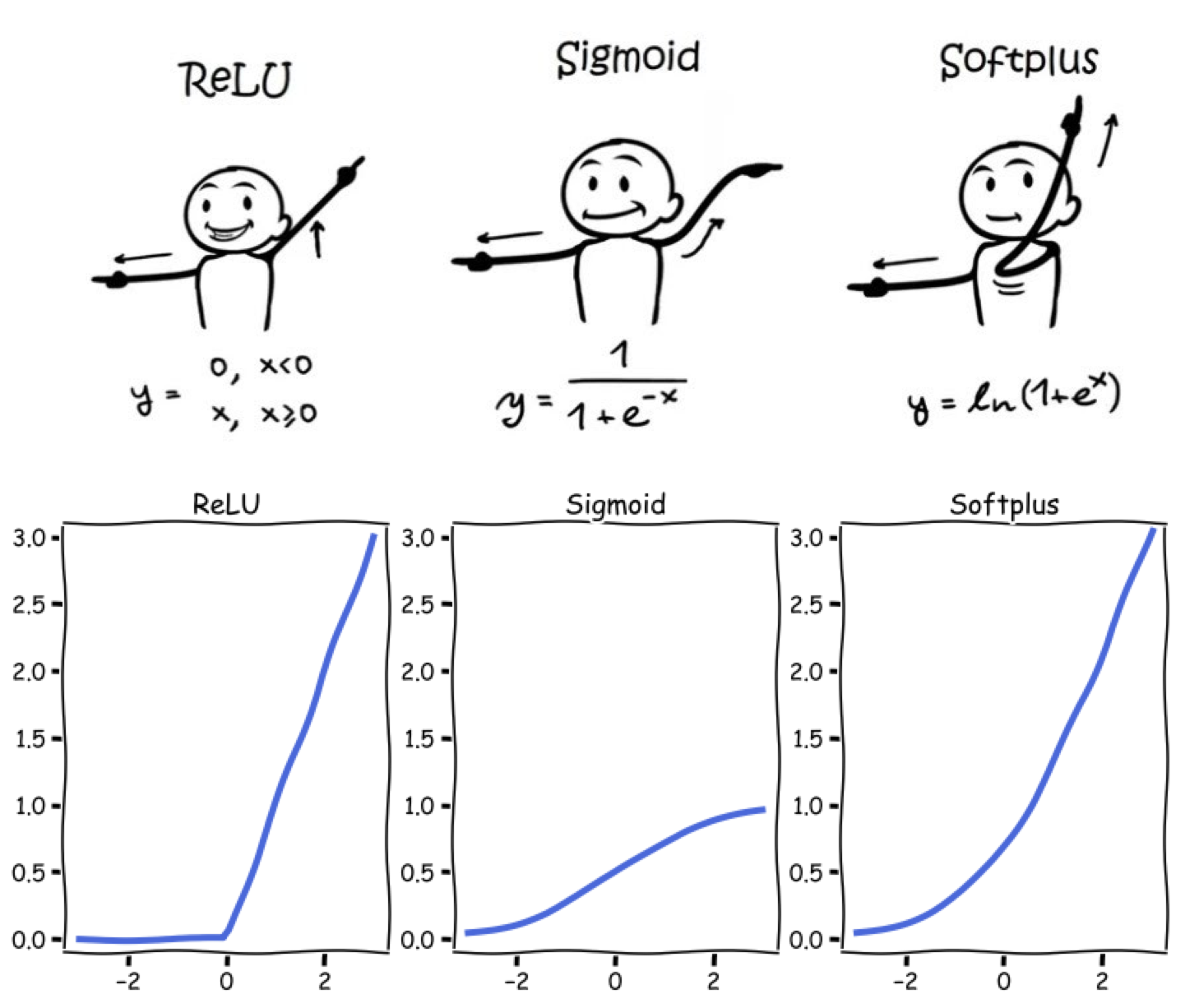
此外，在人工神经网络建模中，我们可以使用各种各样的激活函数，比如ReLU、sigmoid和softplus函数。

激活函数 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Parameter definition
# Hyperparameters
hpar = dict(
    # Task parameters
    dt = 20, # simulation time step [ms]
    stim_len = 1000, # stimulus input duration [ms]
    stim_noise = 0.3, # stimulus input noise [unitless]
    seq_len = 60, # trial duration in time steps
    # Network parameters
    n_neurons = 64, # number of recurrent neurons
    network_noise = 0.1, # noise to network [unitless]
    tau = 100, # network time constant [ms]
    activation_fun = 'relu', # activation function(sigmoid, relu, softplus)
    # Network parameters：training
    batch_size = 16, # size of batch
    n_iteration = 1000, # number of epochs
    learning_rate = 0.01, # training learning rate
    optimizer = 'Adam', # optimizer(Adam, RMSprop, SGD)
    loss = 'CrossEntropy' # loss function(CrossEntropy, L1, L2)
)

batch：指每次迭代中用于训练模型的样本数量。批大小的选择会影响训练的效果和速度。较大的批大小可以提高训练的效率，因为可以同时处理更多的样本，但会消耗更多的内存。较小的批大小可以提供更多的随机性和模型收敛的稳定性，但可能会导致训练时间增加。
iteration：指完成整个训练数据集的一次遍历。迭代的数量取决于训练数据集的大小和训练过程的要求。通常，较大的数据集需要更多的迭代来使模型收敛，而较小的数据集可能需要较少的迭代。

训练 RNN 执行任务

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# make neurogym environment
task_name = 'PerceptualDecisionMaking-v0'
kwargs = {'dt': hpar['dt'],
          'timing': {'stimulus': hpar['stim_len']},
          'sigma': hpar['stim_noise']}
env = gym.make(task_name, **kwargs) 

# make supervised dataset
dataset = ngym.Dataset(env, batch_size=hpar['batch_size'], seq_len=hpar['seq_len'])

# generate one batch of data when called
inputs, target = dataset()
print('Input to network has shape(SeqLen,Batch,Dim)=', inputs.shape)
print('Target to network has shape(SeqLen,Batch)=', target.shape)
# 输出
# Input to network has shape(SeqLen,Batch,Dim)= (60, 16, 3)
# Target to network has shape(SeqLen,Batch)= (60, 16)

gym.make(task_name, **kwargs)：是OpenAI Gym库中用于创建一个与特定任务相关的环境对象。task_name表示要创建的任务的名称，例如CartPole-v1，每个名称对应一个特定的任务环境。**kwargs是一个可选的关键字参数，用于传递额外的配置选项给环境。
在Python中，**用于将一个字典（dictionary）解包为关键字参数传递给函数。字典的关键字需与函数的参数名称匹配，参数顺序可以改变。

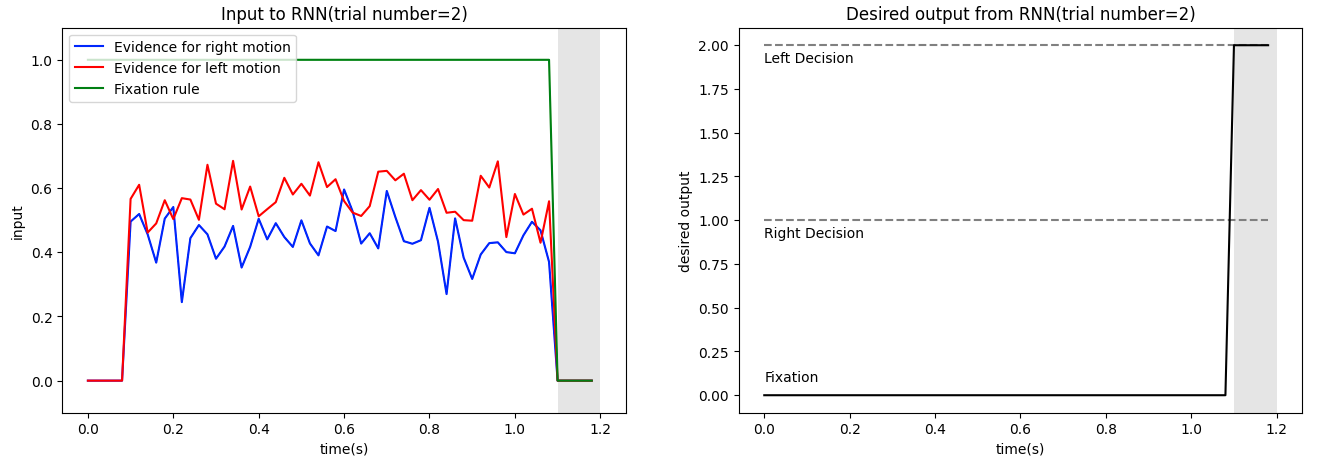
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Task structure
i_trial = np.random.choice(hpar['batch_size']) # 随机从一个batch内选择一个trial
end = sum([v for _,v in env.timing.items()])/1000 # 单位换为s
times = np.arange(end, step=env.dt/1000)
rules = end - env.timing['decision']/1000, end

f, ax = plt.subplots(1, 2, figsize=(16,5))
ax[0].axvspan(rules[0], rules[1], facecolor='grey', alpha=0.2)
ax[0].plot(times, inputs[:,i_trial,1], 'blue', label='Evidence for right motion')
ax[0].plot(times, inputs[:,i_trial,2], 'red', label='Evidence for left motion')
ax[0].plot(times, inputs[:,i_trial,0], 'green', label='Fixation rule')
ax[0].set_ylabel('input')
ax[0].set_ylim([-0.1,1.1])
ax[0].legend(loc='upper left')
ax[0].set_xlabel('time(s)')
ax[0].set_title(f'Input to RNN(trial number={i_trial})')

ax[1].axvspan(rules[0], rules[1], facecolor='grey', alpha=0.2)
ax[1].hlines(y=1, xmin=times[0], xmax=times[-1], color='gray', linestyle="dashed")
ax[1].hlines(y=2, xmin=times[0], xmax=times[-1], color='gray', linestyle="dashed")
ax[1].text(0, 0.08, 'Fixation')
ax[1].text(0, 0.9, 'Right Decision')
ax[1].text(0, 1.9, 'Left Decision')
ax[1].plot(times, target[:,i_trial], 'k')
ax[1].set_ylabel('desired output')
ax[1].set_ylim([-0.1,2.1])
ax[1].set_xlabel('time(s)')
ax[1].set_title(f'Desired output from RNN(trial number={i_trial})')
plt.show()

示例trial的输入和输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# Model definition
class RNN(torch.nn.Module):
  def __init__(self, input_size, output_size, **hpar):
    super().__init__()
    self.input_size = input_size
    self.output_size = output_size
    self.hidden_size = hpar['n_neurons']
    self.noise = hpar['network_noise']
    self.tau = hpar['tau']
    self.alpha = hpar['dt']/self.tau
    self.input2rec = torch.nn.Linear(self.input_size, self.hidden_size, bias=False)
    self.rec2rec = torch.nn.Linear(self.hidden_size, self.hidden_size)
    self.rec2output = torch.nn.Linear(self.hidden_size, self.output_size)
    self.normal = torch.distributions.normal.Normal(0,1)
    self.set_activation_fun(**hpar)

  def set_activation_fun(self, **hpar):
    if hpar['activation_fun'] == 'sigmoid':
      self.activation = torch.sigmoid
    elif hpar['activation_fun'] == 'relu':
      self.activation = torch.relu
    elif hpar['activation_fun'] == 'softplus':
      self.activation = F.softplus
    else:
      raise NotImplementedError('Activation functions should be either ReLU, Sigmoid, or Softplus')

  def init_hidden(self, input_shape):
    batch_size = input_shape[1]
    return torch.zeros(batch_size, self.hidden_size)
  
  def recurrence(self, input, hidden):
    noise = self.noise * self.normal.sample(hidden.shape)
    h_new = self.activation(self.input2rec(input) + self.rec2rec(hidden))
    h_new = hidden * (1-self.alpha) + h_new * self.alpha
    h_new += noise * (2*self.alpha) ** 0.5
    return h_new

  def forward(self, input, hidden=None):
    if hidden is None:
      hidden = self.init_hidden(input.shape).to(input.device)
    rnn_output = []
    steps = range(input.size(0))
    for i in steps:
      hidden = self.recurrence(input[i], hidden)
      rnn_output.append(hidden)
    
    rnn_output = torch.stack(rnn_output, dim=0)
    output = self.rec2output(rnn_output)

    return output, rnn_output

input_size = env.observation_space.shape[0]
print(input_size) # 
output_size = env.action_space.n
net = RNN(input_size, output_size, **hpar)
print(net)
for name, param in net.named_parameters():
  if param.requires_grad:
    print('\t', name, "," , param.data.shape)
# 输出
# RNN(
#   (input2rec): Linear(in_features=3, out_features=64, bias=False)
#   (rec2rec): Linear(in_features=64, out_features=64, bias=True)
#   (rec2output): Linear(in_features=64, out_features=3, bias=True)
# )
# input2rec.weight , torch.Size([64, 3])
# rec2rec.weight , torch.Size([64, 64])
# rec2rec.bias , torch.Size([64])
# rec2output.weight , torch.Size([3, 64])
# rec2output.bias , torch.Size([3])

__init__：在Python中，__init__是一个特殊的方法（也称为构造方法），用于在创建类的实例时进行初始化操作。__init__方法在创建类的实例时自动调用，并用于设置对象的初始状态。它接受类的实例作为第一个参数（通常被命名为self），以便可以访问和操作该实例的属性和方法。除了self参数外，__init__方法可以接受其他参数，这些参数可以用来初始化对象的属性。
super().__init__()：调用父类的构造方法，确保父类的初始化操作得以执行。
Activation function：ReLU、Sigmoid、Softplus
Optimizer：Adam、RMSprop、SGD
loss function：CrossEntropy、L1、L2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
# train model
learning_rate = 0.01
optimizer = 'Adam'
loss_function = 'CrossEntropy'

hpar['learning_rate'] = learning_rate
hpar['optimizer'] = optimizer
hpar['loss_function'] = loss_function

def train_model(net, dataset, **hpar):
  # define an optimizer
  learning_rate = hpar['learning_rate']
  if hpar['optimizer'] == 'Adam':
    optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)
  elif hpar['optimizer'] == 'RMSprop':
    optimizer = torch.optim.RMSprop(net.parameters(), lr=learning_rate)
  elif hpar['optimizer'] == 'SGD':
    optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)
  else:
    raise NotImplementedError('Optimizer should be either Adam, RMSprop, or SGD')
  # define a loss function
  if hpar['loss'] == 'CrossEntropy':
    criterion = torch.nn.CrossEntropyLoss()
  elif hpar['loss'] == 'L1':
    criterion = torch.nn.L1loss()
  elif hpar['loss'] == 'L2':
    criterion = torch.nn.MSELoss()
  else:
    raise NotImplementedError('Loss function should be either CrossEntropy, l1, or L2')

  start_time = time.time()
  losses = []
  accs = []

  # Plot
  fig = plt.figure(figsize=[18,6])
  plt.tight_layout()
  ax0 = fig.add_subplot(121)
  ax0.set_xlim([0,hpar['n_iteration']])
  plt.ylim([0,0.5])
  ax0.set_xlabel('Number of iteration')
  ax0.set_ylabel('Loss')
  ax0.set_title('RNN model training curve')
  ax1 = fig.add_subplot(121, sharex=ax0, frameon=False)
  ax1.yaxis.tick_right()
  ax1.yaxis.set_label_position('right')
  ax1.set_ylabel('Accuracy(%)')
  ax1.set_ylim([0,100])
  ax1.yaxis.label.set_color('r')
  ax0.spines['right'].set_color('r')
  ax1.tick_params(axis='y', colors='r')
  ax2 = fig.add_subplot(122)
  ax2.set_title('RNN model recurrent weight $W_r$')

  # Loop
  for i in range(hpar['n_iteration']):
    inputs, labels = dataset() # 一个batch的数据
    inputs = torch.from_numpy(inputs).type(torch.float)
    labels = torch.from_numpy(labels.flatten()).type(torch.long)

    optimizer.zero_grad() # clear the gradient buffers
    output, _ = net(inputs) # run the network
    output = output.view(-1, output_size)

    if hpar['loss'] == 'CrossEntropy':
      loss = criterion(output, labels)
    else:
      loss = criterion(output, F.one_hot(labels).type(torch.float))
    loss.backward() # backpropagation
    optimizer.step() # gradient descent

    # compute the running loss every 100 steps
    losses.append(loss.item())
    # 将输出张量转换为 NumPy 数组，然后选择最后 hpar['batch_size'] 行，并找到选定数组中每个样本的预测类别的索引。最终，pred 是一个包含每个样本预测类别索引的数组。
    pred = np.argmax(output.detach().numpy()[(-hpar['batch_size']):,:],axis=-1)
    true = labels.detach().numpy()[(-hpar['batch_size']):]
    accs.append((pred==true).mean()*100)

    if i % 100 == 99:
      accs_ma = accs.copy()
      accs_ma[10:] = np.convolve(accs_ma, np.ones(10)/10, mode='valid')

      ax0.plot(losses, color='k', linewidth=2)
      ax1.plot(accs_ma, color='r', linewidth=1)

      recurrent_weight = net.get_parameter('rec2rec.weight').detach().numpy()
      im = ax2.imshow(recurrent_weight, clim=[-0.6,0.6], cmap='RdBu_r')
      ax2.set_xlabel('Presynaptic neuron index')
      ax2.set_ylabel('Postsynaptic neuron index')
      cb = plt.colorbar(im, ax=ax2)

      display.clear_output(wait=True)
      display.display(plt.gcf())
      if i != hpar['n_iteration'] -1:
        cb.remove()
    if i == hpar['n_iteration'] -1:
      display.clear_output(wait=True)
      print(f'Final training loss={np.round(np.mean(losses[(-100):]),2)}')
      print(f'Final training accuracy(%)={np.round(np.mean(accs[(-100):]),2)}')
  return net
net = RNN(input_size, output_size, **hpar)
net = train_model(net, dataset, **hpar)

训练误差及准确率

分析训练好的 RNN 模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Analysis
def run_model(net, env, num_trial=200):
  env.reset(no_step=True)
  input_dict = {}
  activity_dict = {}
  trial_infos = {}
  for i in range(num_trial):
    trial_info = env.new_trial()
    ob, gt = env.ob, env.gt # observation and ground-truth
    inputs = torch.from_numpy(ob[:, np.newaxis, :]).type(torch.float)

    action_pred, rnn_activity = net(inputs)
    action_pred = action_pred.detach().numpy()[:, 0, :]
    choice = np.argmax(action_pred[-1, :])
    correct = choice==gt[-1]

    _input = inputs[:, 0, :].detach().numpy()
    rnn_activity = rnn_activity[:, 0, :].detach().numpy()
    input_dict[i] = _input
    activity_dict[i] = rnn_activity
    trial_infos[i] = trial_info
    trial_infos[i].update({
        'correct': correct,
        'pred': action_pred,
        'target': dataset.env.gt
    })
  return input_dict, activity_dict, trial_infos

run_inputs, activity_dict, trial_infos = run_model(net, dataset.env)
test_acc = np.round(np.mean([val['correct'] for val in trial_infos.values()])*100, 2)
print(f'Testing accuracy(%)={test_acc}')
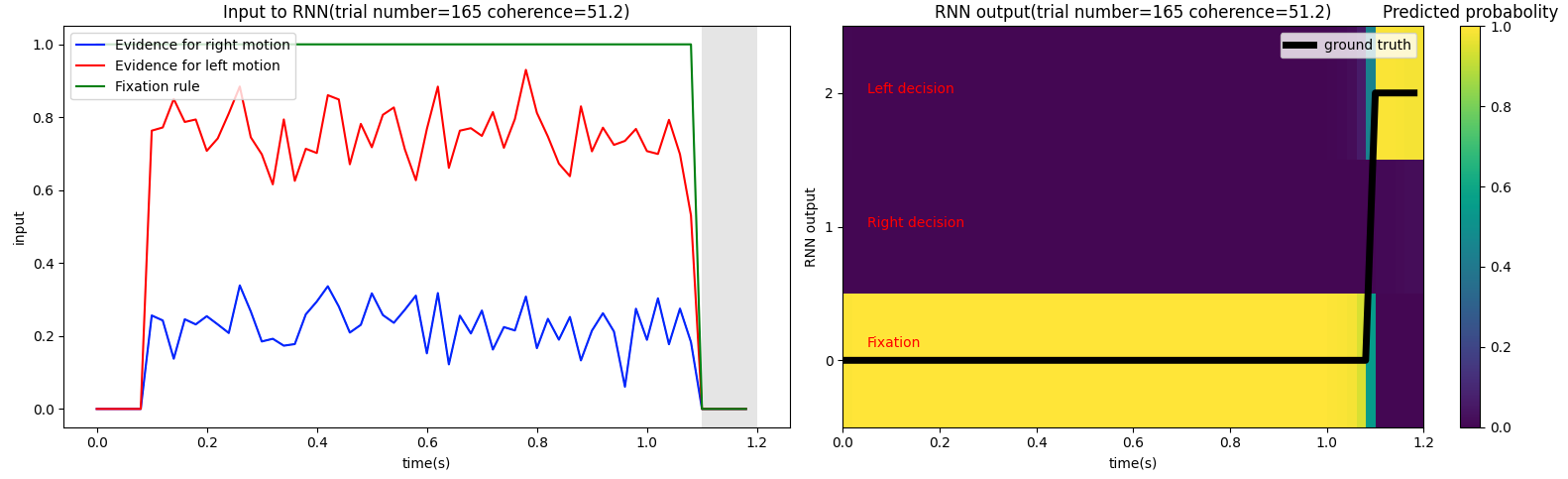
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# randomly choose an example trial
i_trial = np.random.choice(200)
coh = trial_infos[i_trial]['coh']
print(f'coherence={coh}')
# dict_items([('fixation', 100), ('stimulus', 1000), ('delay', 0), ('decision', 100)])
end = sum([v for _,v in env.timing.items()])/1000 
times = np.arange(end, step=env.dt/1000) # 0~(end-1)
rules = end - env.timing['decision']/1000, end

f, ax = plt.subplots(1, 2, figsize=(16,5))
ax[0].axvspan(rules[0], rules[1], facecolor='grey', alpha=0.2)
ax[0].plot(times, run_inputs[i_trial][:,1], 'blue', label='Evidence for right motion')
ax[0].plot(times, run_inputs[i_trial][:,2], 'red', label='Evidence for left motion')
ax[0].plot(times, run_inputs[i_trial][:,0], 'green', label='Fixation rule')
ax[0].legend(loc='upper left')
ax[0].set_xlabel('time(s)')
ax[0].set_ylabel('input')
ax[0].set_title(f'Input to RNN(trial number={i_trial} coherence={coh})')

im = ax[1].imshow(softmax(trial_infos[i_trial]['pred'],axis=-1).T, extent=[times[0],end,-0.5,2.5], aspect='auto', origin='lower')
ax[1].text(0.05,0.1,'Fixation', color='r')
ax[1].text(0.05,1,'Right decision', color='r')
ax[1].text(0.05,2,'Left decision', color='r')
ax[1].plot(times, trial_infos[i_trial]['target'], 'k', linewidth=5, label='ground truth')
ax[1].set_xlabel('time(s)')
ax[1].set_ylabel('RNN output')
ax[1].set_yticks([0,1,2])
ax[1].set_title(f'RNN output(trial number={i_trial} coherence={coh})')
ax[1].legend()

cb = plt.colorbar(im, ax=ax[1])
cb.ax.set_title('Predicted probabolity')
plt.tight_layout()
plt.show()

示例试次输出结果展示

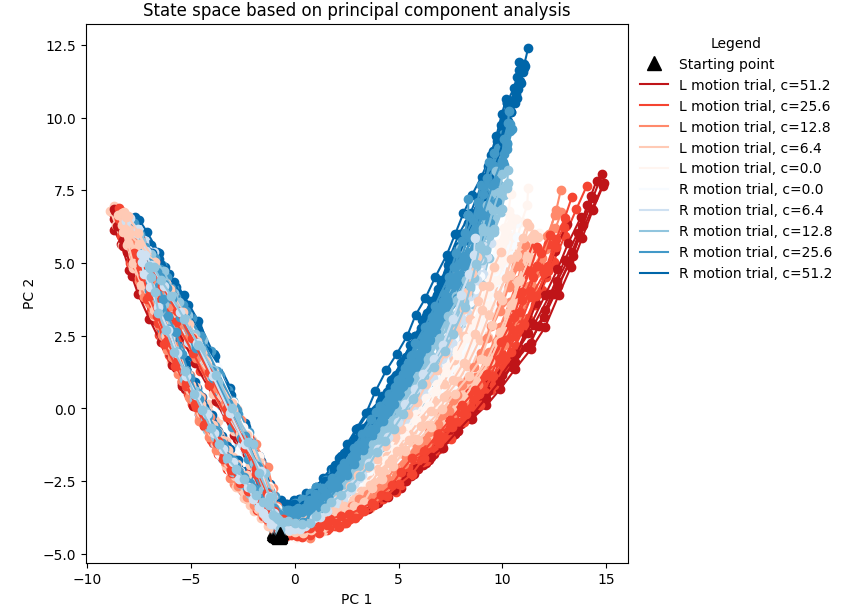
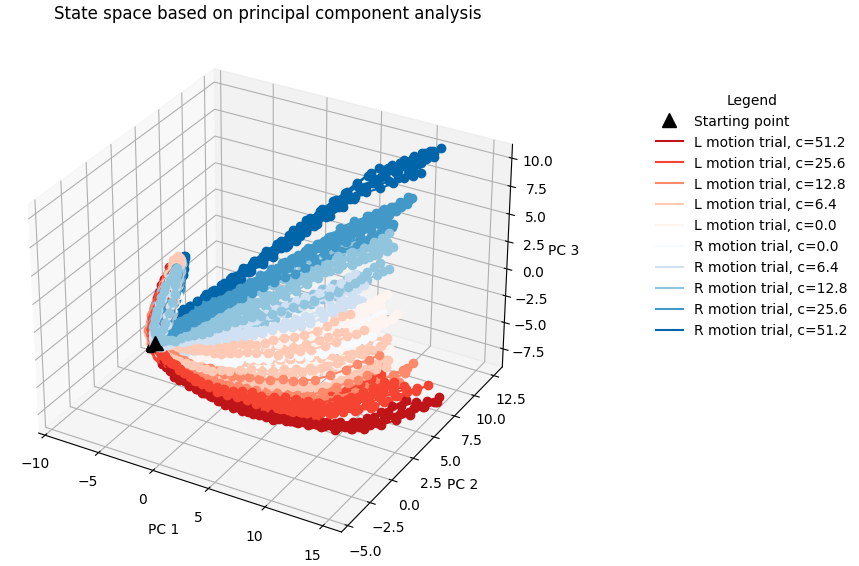
RNN模型测试准确率达到90%以上时，PCA分析不同运动一致比例条件下RNN群体活动轨迹比较容易分开。如果模型的准确率不高，则轨迹比较集中。🦁也就是说，模型是否训练好要设定一个performance threshold~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# PCA(2 principal components)
activity = np.concatenate(list(activity_dict[i] for i in range(200)), axis=0)
pca = PCA(n_components=3)
pca.fit(activity)
activity_pc = pca.transform(activity)

blues = cm.get_cmap('Blues', len(env.cohs)+1)
reds = cm.get_cmap('Reds', len(env.cohs)+1)

figure = plt.figure(figsize=([7,7]))
for i in range(100):
  activity_pc = pca.transform(activity_dict[i])
  trial = trial_infos[i]
  color_c = blues if trial['ground_truth'] == 0 else reds
  color = color_c(np.where(env.cohs == trial['coh'])[0][0])
  plt.plot(activity_pc[:,0], activity_pc[:,1], 'o-', color=color)

  plt.plot(activity_pc[0,0], activity_pc[0,1], '^', color='black', markersize=10)

handles, labels = plt.gca().get_legend_handles_labels()
dot = Line2D([], [], marker='^', label='Starting point', color='black', linestyle='None', markersize=10)
lines = []
for i_coh, v_coh in reversed(list(enumerate(env.cohs))): # index value
  line_r = Line2D([], [], label=f'L motion trial, c={v_coh}', color=reds(i_coh))
  lines.append(line_r)
for i_coh, v_coh in enumerate(env.cohs):
  line_b = Line2D([], [], label=f'R motion trial, c={v_coh}', color=blues(i_coh))
  lines.append(line_b)
handles.extend([dot]+lines)
plt.legend(title='Legend', bbox_to_anchor=(1.4,1.0), handles=handles, frameon=False)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.title('State space based on principal component analysis')
plt.show()
图片说明 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# PCA(3 principal components)
from mpl_toolkits.mplot3d import Axes3D
activity = np.concatenate(list(activity_dict[i] for i in range(200)), axis=0)
pca = PCA(n_components=3)
pca.fit(activity)
activity_pc = pca.transform(activity)

blues = cm.get_cmap('Blues', len(env.cohs)+1)
reds = cm.get_cmap('Reds', len(env.cohs)+1)

fig = plt.figure(figsize=([7,7]))
ax = fig.add_subplot(111, projection='3d')
for i in range(100):
  activity_pc = pca.transform(activity_dict[i])
  trial = trial_infos[i]
  color_c = blues if trial['ground_truth'] == 0 else reds
  color = color_c(np.where(env.cohs == trial['coh'])[0][0])
  ax.plot(activity_pc[:,0], activity_pc[:,1], activity_pc[:,2], 'o-', color=color)

  ax.plot(activity_pc[0,0], activity_pc[0,1], activity_pc[0,2],'^', color='black', markersize=10)

handles, labels = plt.gca().get_legend_handles_labels()
dot = Line2D([], [], marker='^', label='Starting point', color='black', linestyle='None', markersize=10)
lines = []
for i_coh, v_coh in reversed(list(enumerate(env.cohs))): # index value
  line_r = Line2D([], [], label=f'L motion trial, c={v_coh}', color=reds(i_coh))
  lines.append(line_r)
for i_coh, v_coh in enumerate(env.cohs):
  line_b = Line2D([], [], label=f'R motion trial, c={v_coh}', color=blues(i_coh))
  lines.append(line_b)
handles.extend([dot]+lines)
ax.set_xlabel('PC 1')
ax.set_ylabel('PC 2')
ax.set_zlabel('PC 3')
ax.set_title('State space based on principal component analysis')
plt.legend(title='Legend', bbox_to_anchor=(1.6,0.9), handles=handles, frameon=False)
plt.show()

PCA（三个主成分）

补充知识

**kwargs

1
2
3
4
5
6
7
8
9
10
11
kwargs = {'arg1': 10, 'arg3': True, 'arg2': 'hello'}

def example_function(arg1, arg2, arg3):
    print(arg1)
    print(arg2)
    print(arg3)

example_function(**kwargs)
# 10
# hello
# True

字典

在Python中，字典是一种可变的数据结构，用于存储键-值对的集合。字典可以使用{}来创建，也可以通过dict()函数创建。
update方法可以接受一个字典对象或包含键值对的可迭代对象作为参数，并将其中的键值对添加到调用update方法的字典中。

1
2
3
4
5
6
7
8
9
10
11
12
my_dict = {'key1': 'value1', 'key2': 'value2'}
my_dict = dict(
  key1 = value1,
  key2 = value2,
)

my_dict = {'key1': 'value1', 'key2': 'value2'}
new_dict = {'key3': 'value3', 'key4': 'value4'}

my_dict.update(new_dict)
print(my_dict)
# 输出：{'key1': 'value1', 'key2': 'value2', 'key3': 'value3', 'key4': 'value4'}

time.time()

1
2
3
4
5
6
7
import time

start_time = time.time()
for i in range(10):
  print(i)
end_time = time.time() # 可用于计算程序运行的时间
print(f'程序用时：{end_time-start_time}s')

参考内容